Week 10: Regression (continued)

Recall: What is regression about?

• Modeling the relationship between variables
• Response variable (dependent variable, outcome): what we want to predict or explain
• Predictor variable(s) (independent variable(s), explanatory variable(s)): what we use to predict or explain
• Potential goals:
  • Prediction: estimate the response for new observations
  • Inference: understand whether and how predictors affect the response

Multiple regression

Extending to multiple predictors

• Multiple regression includes more than one predictor \[Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_p X_p + \epsilon\]

• Each coefficient \(\beta_j\) represents the effect of \(X_j\) on \(Y\), holding other predictors constant

• R syntax:

model <- lm(response ~ predictor1 + predictor2 + predictor3,
            data = dataset)

Example: mtcars dataset

data(mtcars)
head(mtcars)

                   mpg cyl disp  hp drat    wt  qsec vs am gear carb
Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1
Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1
Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2
Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1

• mpg: miles per gallon
• wt: weight (1000 lbs)
• hp: horsepower
• cyl: number of cylinders

Research question

• How do weight and horsepower jointly affect fuel efficiency (mpg)? \[\text{mpg} = \beta_0 + \beta_1 \times \text{wt} + \beta_2 \times \text{hp} + \epsilon\]

Fitting the multiple regression model

mtcars_model <- lm(mpg ~ wt + hp, data = mtcars)
summary(mtcars_model)

Call:
lm(formula = mpg ~ wt + hp, data = mtcars)

Residuals:
   Min     1Q Median     3Q    Max 
-3.941 -1.600 -0.182  1.050  5.854 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 37.22727    1.59879  23.285  < 2e-16 ***
wt          -3.87783    0.63273  -6.129 1.12e-06 ***
hp          -0.03177    0.00903  -3.519  0.00145 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.593 on 29 degrees of freedom
Multiple R-squared:  0.8268,    Adjusted R-squared:  0.8148 
F-statistic: 69.21 on 2 and 29 DF,  p-value: 9.109e-12

Interpreting multiple regression coefficients

coef(mtcars_model)

(Intercept)          wt          hp 
37.22727012 -3.87783074 -0.03177295 

• Intercept (\(\hat{\beta}_0 = 37.23\)): expected mpg when weight and horsepower are both 0 (not meaningful)
• wt (\(\hat{\beta}_1 = -3.88\)): for each 1000 lb increase in weight, mpg decreases by about 3.88, holding horsepower constant
• hp (\(\hat{\beta}_2 = -0.03\)): for each 1 hp increase, mpg decreases by about 0.03, holding weight constant

Comparing models

• We can compare models with different numbers of predictors

# Simple model: mpg vs weight only
model1 <- lm(mpg ~ wt, data = mtcars)

# Multiple model: mpg vs weight and horsepower
model2 <- lm(mpg ~ wt + hp, data = mtcars)

# Compare R-squared
summary(model1)$r.squared

[1] 0.7528328

summary(model2)$r.squared

[1] 0.8267855

• Model 2 explains more variance (higher R-squared)

ANOVA for model comparison

anova(model1, model2)

Analysis of Variance Table

Model 1: mpg ~ wt
Model 2: mpg ~ wt + hp
  Res.Df    RSS Df Sum of Sq      F   Pr(>F)   
1     30 278.32                                
2     29 195.05  1    83.274 12.381 0.001451 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• The ANOVA F-test compares the two models
• Small p-value indicates that adding hp significantly improves the model
• The more complex model (model2) is preferred

Categorical predictors

Including categorical variables

• Categorical predictors are automatically converted to dummy variables
• Example: modeling mpg as a function of number of cylinders
  • cyl can be 4, 6, or 8

mtcars$cyl <- factor(mtcars$cyl)
cyl_model <- lm(mpg ~ cyl, data = mtcars)
summary(cyl_model)

Call:
lm(formula = mpg ~ cyl, data = mtcars)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.2636 -1.8357  0.0286  1.3893  7.2364 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  26.6636     0.9718  27.437  < 2e-16 ***
cyl6         -6.9208     1.5583  -4.441 0.000119 ***
cyl8        -11.5636     1.2986  -8.905 8.57e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.223 on 29 degrees of freedom
Multiple R-squared:  0.7325,    Adjusted R-squared:  0.714 
F-statistic:  39.7 on 2 and 29 DF,  p-value: 4.979e-09

Interpreting categorical coefficients

coef(cyl_model)

(Intercept)        cyl6        cyl8 
  26.663636   -6.920779  -11.563636 

• R creates dummy variables with the first level as the reference category
  • Here, 4 cylinders is the reference
• Intercept (\(\hat{\beta}_0 = 26.66\)): mean mpg for 4-cylinder cars
• cyl6 (\(\hat{\beta}_1 = -6.92\)): 6-cylinder cars have about 6.92 lower mpg than 4-cylinder cars, on average
• cyl8 (\(\hat{\beta}_2 = -11.56\)): 8-cylinder cars have about 11.56 lower mpg than 4-cylinder cars, on average

Visualizing categorical regression

ggplot(mtcars, aes(x = cyl, y = mpg, fill = cyl)) +
  geom_boxplot(alpha = 0.5) +
  stat_summary(fun = mean, geom = "point", shape = 18, size = 4, color = "red") +
  labs(title = "MPG by number of cylinders",
       subtitle = "Red diamonds show group means (regression estimates)",
       x = "Number of cylinders", y = "Miles per gallon") +
  theme_minimal() +
  theme(legend.position = "none")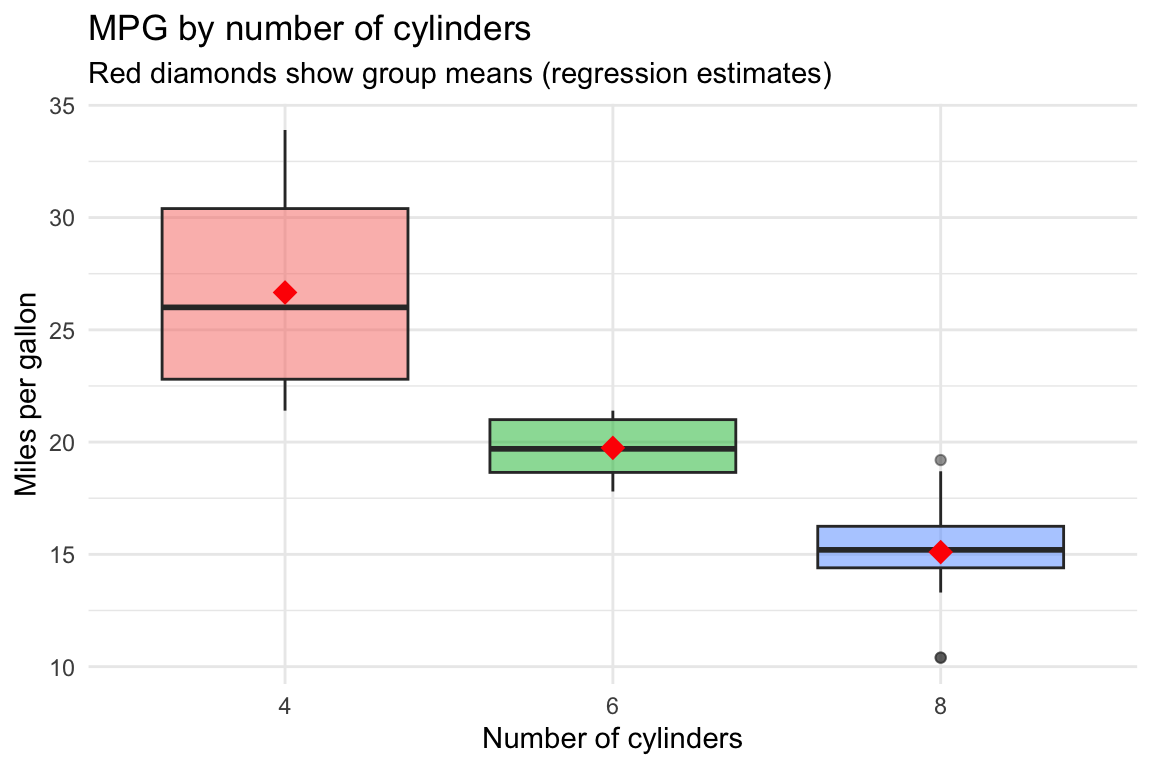

Key R functions for regression

Summary table

Function	Purpose	Example
lm()	Fit linear model	lm(y ~ x, data = df)
summary()	Model summary statistics	summary(model)
coef()	Extract coefficients	coef(model)
confint()	Confidence intervals	confint(model)
predict()	Make predictions	predict(model, newdata)
plot()	Diagnostic plots	plot(model)
anova()	Compare models	anova(model1, model2)

Formula syntax in R

Formula	Meaning
y ~ x	Simple regression: y on x
y ~ x1 + x2	Multiple regression: y on x1 and x2
y ~ x1 + x2 + x1:x2	Include interaction between x1 and x2
y ~ x1 * x2	Equivalent to y ~ x1 + x2 + x1:x2
y ~ .	Use all other variables as predictors
y ~ x - 1	Regression without intercept

Important considerations

Correlation vs. causation

• Regression reveals associations, not necessarily causation
• Just because \(X\) predicts \(Y\) doesn’t mean \(X\) causes \(Y\)
• Possible explanations for correlation:
  1. \(X\) causes \(Y\)
  2. \(Y\) causes \(X\)
  3. A third variable causes both \(X\) and \(Y\) (confounding)
  4. The association is due to chance
• Randomized experiments (like the clinical trials in Week 4) provide stronger evidence for causation

Extrapolation

• Extrapolation: making predictions outside the range of observed data
• The linear relationship may not hold beyond the observed range
• Example: predicting stopping distance for a car going 100 mph using our cars model
  • The data only include speeds from 4 to 25 mph
  • Extrapolating to 100 mph is risky

Limitations of R-squared

• R-squared measures the proportion of variance explained
• Higher R-squared doesn’t always mean a better model:
  • Adding more predictors always increases R-squared
  • A model with lower R-squared might generalize better
  • R-squared doesn’t tell us if the model assumptions are met
• Use adjusted R-squared when comparing models with different numbers of predictors
  • Penalizes for adding unnecessary predictors

Example: Full analysis

Palmer Penguins dataset

if(!require(palmerpenguins)) install.packages("palmerpenguins")
library(palmerpenguins)
data(penguins)
str(penguins)

tibble [344 × 8] (S3: tbl_df/tbl/data.frame)
 $ species          : Factor w/ 3 levels "Adelie","Chinstrap",..: 1 1 1 1 1 1 1 1 1 1 ...
 $ island           : Factor w/ 3 levels "Biscoe","Dream",..: 3 3 3 3 3 3 3 3 3 3 ...
 $ bill_length_mm   : num [1:344] 39.1 39.5 40.3 NA 36.7 39.3 38.9 39.2 34.1 42 ...
 $ bill_depth_mm    : num [1:344] 18.7 17.4 18 NA 19.3 20.6 17.8 19.6 18.1 20.2 ...
 $ flipper_length_mm: int [1:344] 181 186 195 NA 193 190 181 195 193 190 ...
 $ body_mass_g      : int [1:344] 3750 3800 3250 NA 3450 3650 3625 4675 3475 4250 ...
 $ sex              : Factor w/ 2 levels "female","male": 2 1 1 NA 1 2 1 2 NA NA ...
 $ year             : int [1:344] 2007 2007 2007 2007 2007 2007 2007 2007 2007 2007 ...

Research question

• How does body mass depend on flipper length and species?
• Let’s build a multiple regression model

Exploratory visualization

ggplot(penguins, aes(x = flipper_length_mm, y = body_mass_g, color = species)) +
  geom_point(size = 2, alpha = 0.6) +
#   geom_smooth(method = "lm", se = FALSE) +
  labs(title = "Body mass vs. flipper length by species",
       x = "Flipper length (mm)", y = "Body mass (g)") +
  theme_minimal()

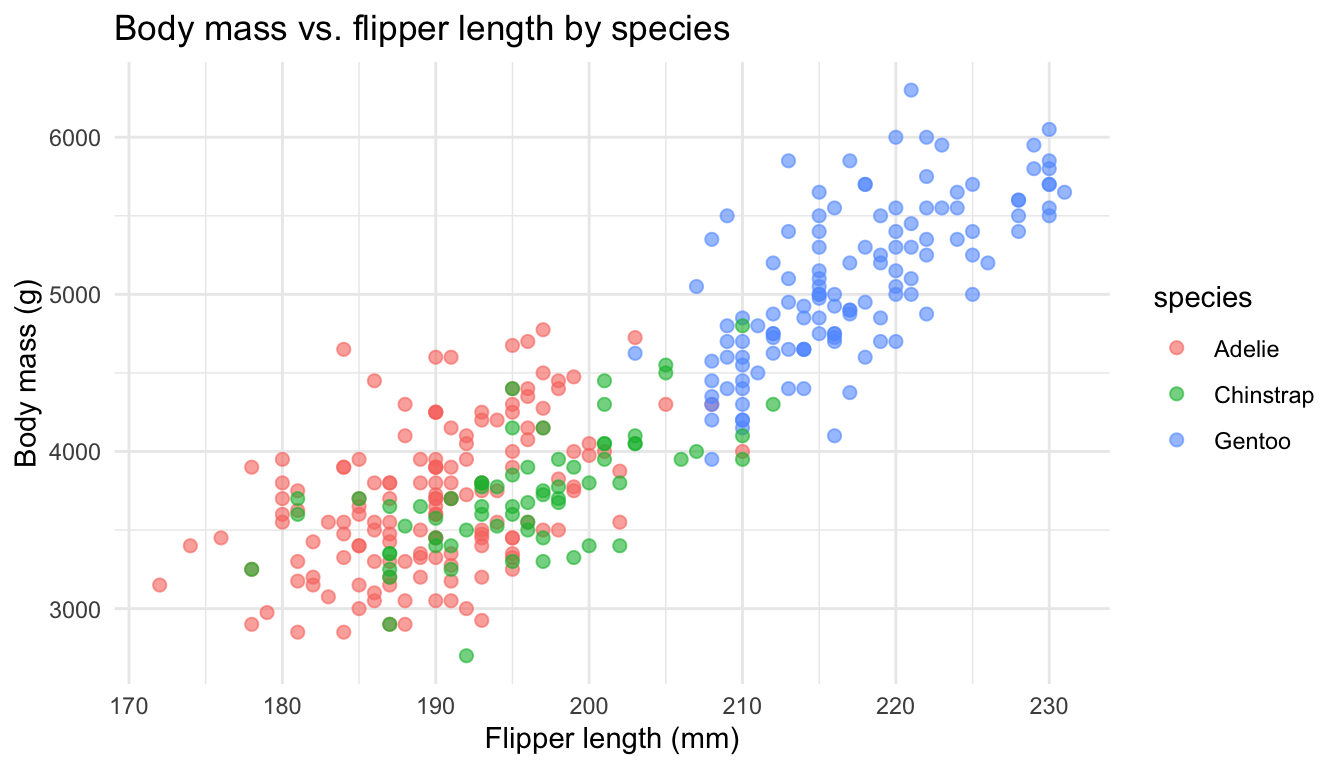
Fitting the model

# Remove missing values
penguins_clean <- na.omit(penguins[, c("body_mass_g", "flipper_length_mm", "species")])

# Fit model
penguin_model <- lm(body_mass_g ~ flipper_length_mm + species, data = penguins_clean)
summary(penguin_model)

Call:
lm(formula = body_mass_g ~ flipper_length_mm + species, data = penguins_clean)

Residuals:
    Min      1Q  Median      3Q     Max 
-927.70 -254.82  -23.92  241.16 1191.68 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)       -4031.477    584.151  -6.901 2.55e-11 ***
flipper_length_mm    40.705      3.071  13.255  < 2e-16 ***
speciesChinstrap   -206.510     57.731  -3.577 0.000398 ***
speciesGentoo       266.810     95.264   2.801 0.005392 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 375.5 on 338 degrees of freedom
Multiple R-squared:  0.7826,    Adjusted R-squared:  0.7807 
F-statistic: 405.7 on 3 and 338 DF,  p-value: < 2.2e-16

Interpreting the results

coef(penguin_model)

      (Intercept) flipper_length_mm  speciesChinstrap     speciesGentoo 
       -4031.4769           40.7054         -206.5101          266.8096 

• Intercept: Expected body mass for Adelie penguin with 0 mm flipper length (not meaningful)
• flipper_length_mm: For each 1 mm increase in flipper length, body mass increases by about 40.7 g, holding species constant
• speciesChinstrap: Chinstrap penguins are about 206.5 g lighter than Adelie, holding flipper length constant
• speciesGentoo: Gentoo penguins are about 266.8 g heavier than Adelie, holding flipper length constant

Model diagnostics

par(mfrow = c(2, 2))
plot(penguin_model)

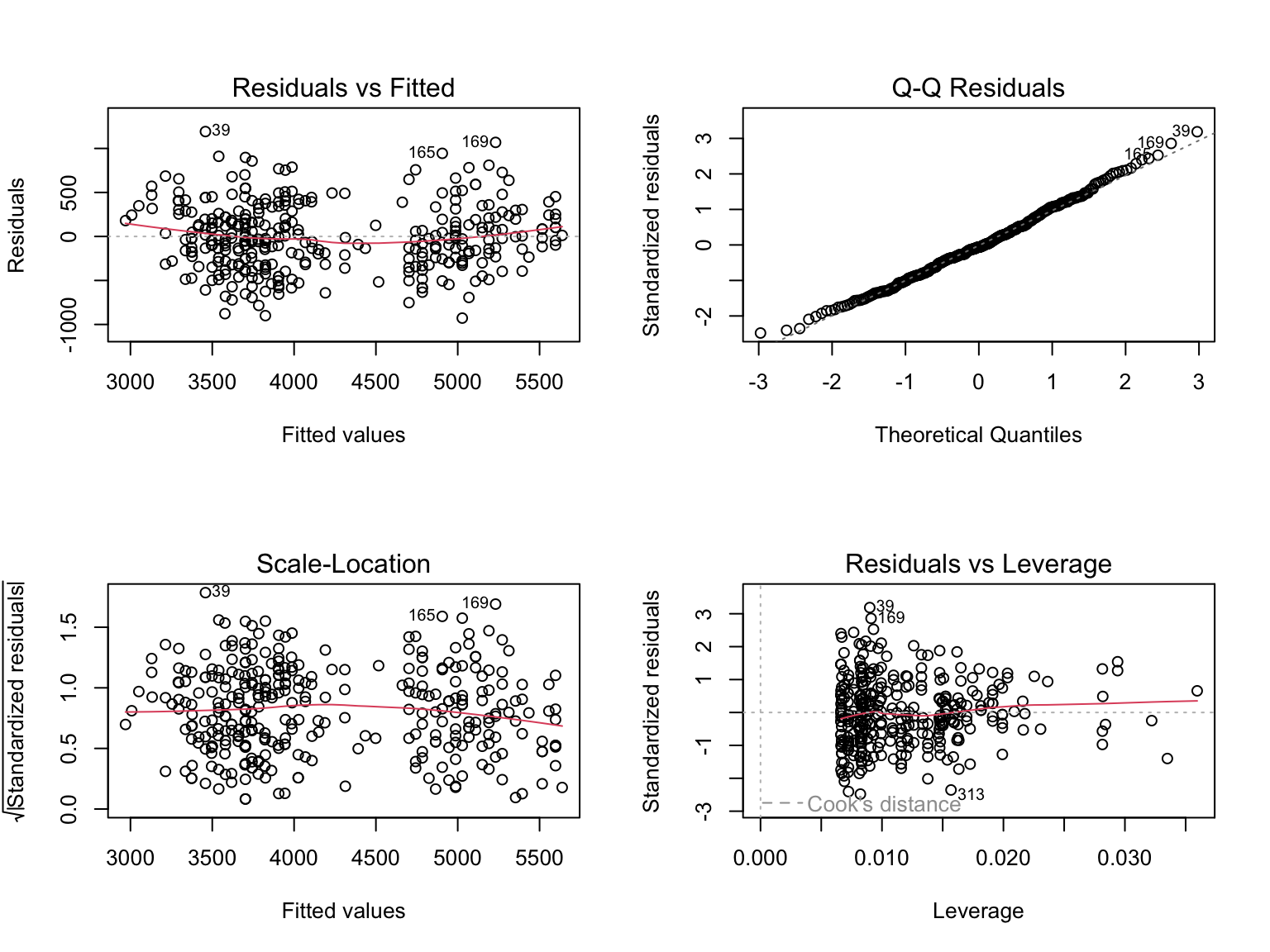
Making predictions

# Predict body mass for a Gentoo penguin with 210 mm flippers
new_penguin <- data.frame(
  flipper_length_mm = 210,
  species = "Gentoo"
)

predict(penguin_model, newdata = new_penguin, interval = "prediction")

       fit     lwr      upr
1 4783.467 4040.52 5526.413

• We predict a Gentoo penguin with 210 mm flippers will have a body mass around 4783 g
• The 95% prediction interval is (4041, 5526) g

The two cultures

Two approaches to statistical modeling

Leo Breiman (2001) identified two cultures in statistical modeling:

Culture 1: Data Modeling

• Focus on inference
• Assume a stochastic model (e.g., linear regression)
• Estimate parameters and test hypotheses
• Interpretability is key
• Assumptions matter greatly
• This lecture has focused here

Culture 2: Algorithmic Modeling

• Focus on prediction
• Treat the data mechanism as unknown
• Prioritize predictive accuracy
• “Black box” models acceptable
• Less concern about distributional assumptions
• The box-office prediction case study has some of this flavor

Implications for your work

• In prediction tasks:
  • Diagnostic plots are less critical if the model predicts well on new data
  • Large sample sizes can overcome some assumption violations
  • Cross-validation and test set performance matter more than p-values
  • The “true” model may be unknowable and that’s okay
• In inference tasks (like much of today):
  • Understanding relationships is the goal
  • Assumptions must be checked carefully
  • Coefficient interpretation requires proper model specification
  • Causal claims require even stronger assumptions

Summary

Key takeaways

1. Regression models relationships between variables
2. Simple linear regression: one predictor, estimates slope and intercept
3. Multiple regression: multiple predictors, each coefficient represents effect holding others constant
4. R function: lm(response ~ predictors, data = dataset)
5. Use summary(), coef(), confint(), and predict() to interpret results
6. Check model assumptions using diagnostic plots
7. Categorical predictors are handled automatically via dummy variables
8. Remember: correlation ≠ causation